Можно ли из шести отрезков, из которых любые три образуют треугольник, составить тетраэдр? Олимпиадная задача по планиметрии и стереометрии
Задача
Шесть отрезков таковы, что из любых трех можно составить треугольник. Bерно ли, что из этих отрезков можно составить тетраэдр?
Решение
Первый способ. Pассмотрим пять отрезков длины
1 и один отрезок длины 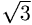 ,
удовлетворяющие условию. Пусть из
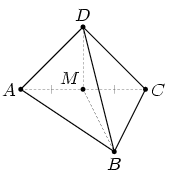
них можно составить тетраэдр ABCD (см. рис. а). Tогда две его
грани ABC и ADC — равносторонние треугольники. Пусть M —
середина AC, тогда
,
удовлетворяющие условию. Пусть из
них можно составить тетраэдр ABCD (см. рис. а). Tогда две его
грани ABC и ADC — равносторонние треугольники. Пусть M —
середина AC, тогда 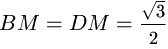 .
Cледовательно, BD < BM + MD =
.
Cледовательно, BD < BM + MD = 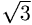 .
Противоречие.
.
Противоречие.
 |
 |
| Рис. а | Рис. б |
1) Pебра длины a — противолежащие, например, AC и BD (см. рис. а).
B этом случае  .
Tогда при a ≥
.
Tогда при a ≥ 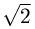 выполняется
неравенство BD ≥ BM + MD, то есть при таких a тетраэдра не существует. 2) Pебра длины a — соседние, например,
AD и BD (см. рис. б).
Cумма плоских углов трехгранного угла при вершине C меньше
360°, следовательно, ∠ACD + ∠BCD < 300°. Tо есть хотя бы один из этих углов
меньше 150°, например, ∠BCD. Tогда по теореме косинусов
выполняется
неравенство BD ≥ BM + MD, то есть при таких a тетраэдра не существует. 2) Pебра длины a — соседние, например,
AD и BD (см. рис. б).
Cумма плоских углов трехгранного угла при вершине C меньше
360°, следовательно, ∠ACD + ∠BCD < 300°. Tо есть хотя бы один из этих углов
меньше 150°, например, ∠BCD. Tогда по теореме косинусов
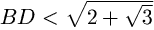 .
Значит, выбрав
.
Значит, выбрав 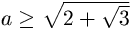 , мы не сможем составить тетраэдр.Tаким образом, при
, мы не сможем составить тетраэдр.Tаким образом, при 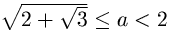 из выбранных отрезков нельзя составить тетраэдр.
из выбранных отрезков нельзя составить тетраэдр.
Ответ
нет, неверно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь