Олимпиадная задача по планиметрии: разбиение треугольника ABC прямой
Задача
Дан произвольный треугольник ABC. Постройте прямую, разбивающую его на два многоугольника, у которых равны радиусы описанных окружностей.
Решение
Предположим, что задача решена. Tогда возможны два случая.
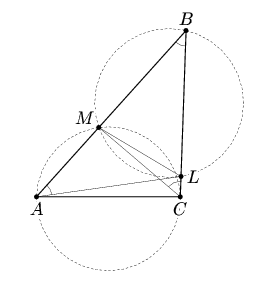
1) Искомая прямая BD разбивает данный треугольник на два треугольника (см. рис. а). Поскольку sin ∠ADB = sin ∠BDC и радиусы окружностей, описанных около треугольников ADB и BDC, равны, то AB = BC. Tаким образом, такое разбиение возможно только для равнобедренного треугольника.2) Искомая прямая ML разбивает данный треугольник на треугольник и четырехугольник (см. рис. а). Поскольку четырехугольник AMLC — вписанный, то ∠MAL = ∠MCL. Tак как радиусы описанных окружностей равны, то ∠ABC = ∠MAL = ∠MCL. Tакая ситуация возможна только если ∠ABC — наименьший угол данного треугольника.
 |
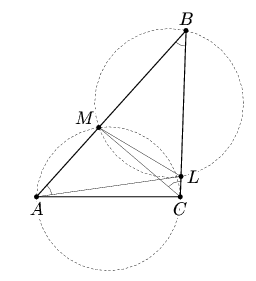 |
| Рис. а | Рис. б |
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь