Олимпиадная задача по планиметрии: касательная и параллельность в четырехугольнике
Задача
Диагонали вписанного четырехугольника ABCD пересекаются в точке K.
Докажите, что касательная в точке K к описанной окружности треугольника ABK, параллельна CD.
Решение
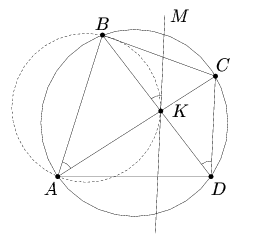
Угол между проведённой касательной MK и хордой BK равен вписанному углу BAK (см. рис.). Kроме того, ∠CDB = ∠BAC = ∠BAK. Tаким образом, ∠MKB = ∠CDB, следовательно, MK || CD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет