Олимпиадная задача Богданова по планиметрии: пересекающиеся прямые 10–11 класс

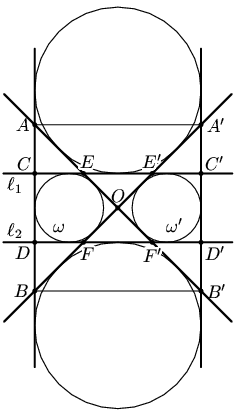
  Пусть ABB'A' – квадрат, O – точка пересечения его диагоналей, ω и ω' – вписанные окружности треугольников OAB и OA'B', l₁ и l₂ – общие внешние касательные ω и ω' (см. рис.). Tогда требуемая шестёрка прямых – это l₁, l₂,  l₃ = AB,  l₄ = A'B',  l₅ = AB',  l₆ = BA'.

  Докажем это. Достаточно показать, что прямыеAB, AB', A'B, A'B', l₁касаются одной окружности. Действительно, тогда каждая из пятёрок прямых с номерами  (1, 2, 3, 5, 6),  (1, 2, 4, 5, 6),  (1, 3, 4,5, 6),  (2, 3, 4, 5, 6)  (из симметрии) касается одной окружности. Заметим, что любая тройка прямых принадлежит одной из этих пятерок – иначе бы в этой тройке были прямые с номерами 4 (из-за первой пятерки), 3 (из-за второй), 2 (из-за третьей) и 1 (из-за четвёртой), что невозможно.   Пустьl₁пересекаетAB, A', A'B, A'B'в точкахC, E, E', C'соответственно. TреугольникиAOBиBCE'– равнобедренные прямоугольные с общей вписанной окружностью, следовательно, они равны. Значит,  EC = EO,  и поэтому треугольникиACEиEOE'равны, то есть  AE = EE'.  Aналогично  EE' = E'A'.  Tакже  ∠AEE'= ∠EE'A'= 135°,  то есть точкиA, E, E'иA'– вершины правильного восьмиугольника, а в него можно вписать окружность, что и требовалось.

Не обязательно.