Олимпиадная задача по планиметрии для 9–10 класса от Заславского А. А.
Задача
В треугольнике ABC M – точка пересечения медиан, O – центр вписанной окружности, A', B', C' – точки ее касания со сторонами BC, CA, AB соответственно. Докажите, что, если CA' = AB, то прямые OM и AB перпендикулярны.
Решение
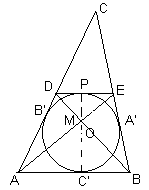
Первый способ. Пусть D и E – середины сторон AC и BC, тогда M – точка пересечения отрезков AE и BD (см. рис. а). Используя равенство отрезков касательной, проведенных из одной точки к окружности, получим, что CA' = ½(AC + BC – AB) = AB (по условию). Следовательно, AD + BE = ½(AC + BC) = 1,5AB = AB + DE, то есть, трапеция ABЕD описана вокруг вписанной окружности треугольника ABC. Пусть P – точка касания окружности с прямой DE. Тогда AC' = AB – BC' = CA' – BA' = (0,5BC + EA') – (0,5BC – EA') = 2EA' = 2EP. Рассмотрим гомотетию с центром М и коэффициентом k = –0,5: образом точки А является точка Е, а образом точки С' – точка Р, поэтому, C'P проходит через точку M. Кроме того, отрезок C'P – общий перпендикуляр к основаниям АВ и DE трапеции, проходящий через точку О, значит, OM и AB перпендикулярны, что и требовалось доказать.
 |
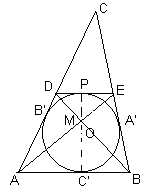 |
| Рис. а | Рис. б |
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь