Олимпиадная задача по планиметрии для 9-10 класса: точки на окружности, Калинин Д. А.
Задача
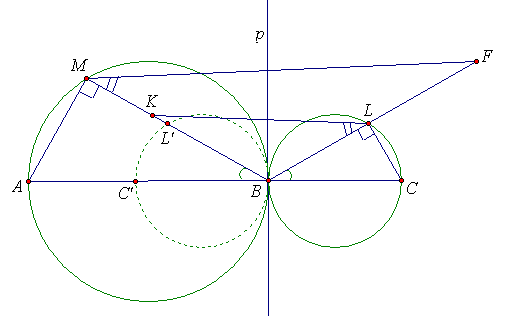
Внутри отрезка АС выбрана произвольная точка В и построены окружности с диаметрами АВ и ВС. На окружностях (в одной полуплоскости относительно АС) выбраны соответственно точки M и L так, что ∠MBA = ∠LBC. Точки K и F отмечены соответственно на лучах ВМ и BL так, что
BK = BC и BF = AB. Докажите, что точки M, K, F и L лежат на одной окружности.
Решение
Заметим, что треугольники ABM и CBL подобны по двум углам, следовательно, BM : BL = AB : CB = BF : BK. Поэтому и треугольники BMF и BLK подобны, так как угол В у них общий, а стороны, заключающие этот угол, – пропорциональны. Следовательно, ∠FМВ = ∠KLВ, то есть
∠FМK + ∠FLK = 180°, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет