Олимпиадная задача по планиметрии для 8-9 класса: прямая BH в четырехугольнике

  Так как угол BAC – острый, то угол CAD – острый, поэтому треугольник AСD – остроугольный. Значит, H – внутренняя точка отрезка АС.

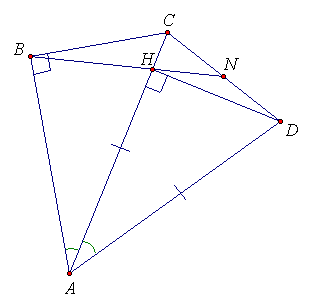
  Пусть N – точка пересечения прямой BH и отрезка CD (см. рис.). Так как треугольники ABC и AHD равны (по гипотенузе и острому углу), то  AB = AH,  то есть треугольник ABH – равнобедренный. Пусть  ∠HBA = α,  тогда  ∠CHN = ∠BHA = α  и  ∠ACN = ½ (180° – ∠CAD) = ½ (180° – ∠CAB) = α,

∠NHD = 90° – α = ∠NDH.  Таким образом,  CN = HN = DN,  поэтому HN – медиана треугольника CHD.

1 : 1.