Построение треугольника по стороне, противолежащему углу и медиане. Олимпиадная задача

Пусть искомый треугольник АВС, в котором: BС = a; ∠BAC = α; BM = m (M – середина АС), построен (см. рис.). Вершина А лежит на дуге ВС окружности с центром О, описанной около треугольника, то есть, принадлежит ГМТ, из которых данный отрезок ВС виден под заданным углом α. Точка М находится на заданном расстоянии m от точки В, то есть, лежит на окружности с центром В и радиусом m. Кроме того, точка М является серединой хорды АС, поэтому ∠ОМС = 90°, то есть, эта точка лежит на окружности с диаметром ОС.Таким образом, этапы построения:1) отрезок ВС длиной а;

2. ГМТ, из которых ВС виден под углом α (одна из дуг окружности с центром О);

3. окружность с центром В и радиусом m;

4. окружность диаметром ОС;

5) М – точка пересечения окружностей пунктов 3) и 4);

6. А – точка пересечения луча СМ с дугой ВС окружности пункта 2);

7. АВС – искомый треугольник.

   
   Тот факт, что М лежит на окружности с диаметром ОС, можно было получить иначе. Так как М – геометрическое место середин хорд СА, где точка С – фиксирована, то М является образом точки А при гомотетии с центром С и коэффициентом 0,5. Поэтому, образом окружности с центром О при этой гомотетии является окружность с центром Q – серединой отрезка ОС.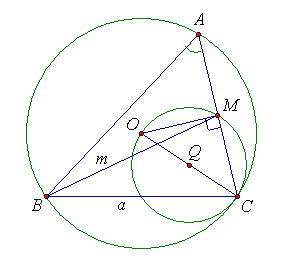

Ответ задачи отсутствует