Олимпиадная задача по планиметрии для 10-11 класса от Блинкова Ю. А.: Точки и высоты в неравнобедренном треугольнике

Решение 1:   Отметим, что CH – диаметр описанной окружности треугольника A₁B₁C (H – ортоцентр).

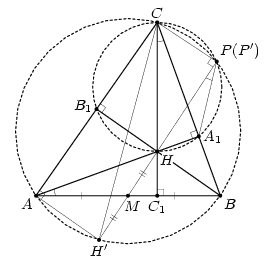
  Докажем несколько вспомогательных утверждений.   1) Точки M (середина AB), H и P лежат на одной прямой (рис. слева).

  Пусть H' симметрична H относительно M, а P' – точка пересечения прямой MH с описанной окружностью треугольника ABC. Тогда, в силу равенства углов при симметрии, H' лежит на описанной окружности, а в силу параллельности центрально симметричных прямых BH и AH',  ∠CAH' = 90°, то есть CH' – диаметр окружности, а значит,  ∠CP'H' = 90°.  Это означает, что описанная окружность треугольника A₁B₁C проходит через P', то есть P' совпадает с P.   2) Описанная окружность треугольника AMA₁ проходит через точку P.

  Используя равенство вписанных углов и 1), получим, что  ∠MAA₁ = ∠HCA₁ = ∠HPA₁ = ∠MPA₁,  что и требовалось.

  3) Точки A, P и точка A₂, симметричная A₁ относительно высоты CC₁, лежат на одной прямой (рис. справа).

  MA = MA₁  (A₁M – медиана прямоугольного треугольника AA₁B). Отсюда, учитывая 2), следует, что PM – биссектриса угла APA₁, то есть A₂ – точка пересечения AP и окружности с диаметром CH.

  Кроме того, CC₁ – биссектриса угла A₁C₁B₁ (см. задачу 152866), откуда следует, что A₂ лежит на прямой B₁C₁.   4)  B₁C₁ || AZ,  A₁C₁ || BZ,  A₂A₁ || AB  (рис. снизу).

  Действительно,  ∠BAZ = ∠ACB = ∠B₁C₁A,  откуда  B₁C₁ || AZ.  Aналогично  A₁C₁ || BZ.  Третья параллельность следует из способа построения точки A₂.

  У равнобедренных треугольников AZB и A₂C₁A₁ соответствующие стороны параллельны, следовательно эти треугольники гомотетичны, причём центр гомотетии лежит на пересечении прямых AA₂, BA₁ и ZC₁. Это и значит, что прямые AP, BC и ZC₁ пересекаются в одной точке.

Решение 2:   Пусть Q – точка пересечения A₁B₁ с AB. Заметим, что A₁ и B₁ лежат на окружности с диаметром AB. Значит, Q – радикальный центр описанных окружностей треугольников ABC и CA₁B₁ и четырёхугольника ABA₁B₁, то есть Q лежит на прямой CP.

  Теперь утверждение задачи очевидно из свойств полярных преобразований: все нужные точки лежат на поляре Q. Действительно, поляра Q проходит через полюс прямой AB – точку Z. Kроме того, она проходит через точку C₁, поскольку двойное отношение точек A, B, C₁, Q равно –1 (теорема о полном четырёхстороннике для точек C, A₁, B₁ и H, см. задачу 158441). Значит, прямая ZC₁ и есть поляра точки Q. То, что поляра точки (Q) пересечения противоположных сторон четырёхугольника (ABPC) проходит через точку пересечения его диагоналей (AP и BC), завершает доказательство.

Ответ задачи отсутствует