Олимпиадная задача по геометрии: угол BDC в выпуклом четырёхугольнике ABCD

Решение 1:   Пусть K и M – точки пересечения прямой CB с прямой AD и описанной окружностью треугольника ACD соответственно (см. рис.). Тогда

∠MDA = ∠MCA = 10°,  то есть DM – биссектриса угла KDB. Также заметим, что  ∠ABD = 50°,  ∠CBD = 80°,  значит  ∠KBA = 50°,  то есть BA – биссектриса угла KBD.

  Итак, I – точка пересечения биссектрис BA и DM – центр вписанной окружности треугольника KBD.  ∠BID = 120°,– поэтому  ∠BKD = 60°.  Значит, четырёхугольник KAIM – вписанный, причём KI – биссектриса угла AKM. Cледовательно,  ∠ACD = ∠AMD = ∠AMI = ∠AKI = 30°,  откуда  ∠BDC = 60°.

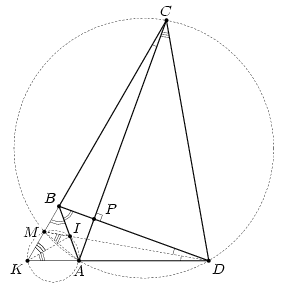
Решение 2:   Пусть P – точка пересечения AC и BD. Заметим, что 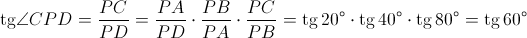    (см. задачу 161203). Cледовательно,  ∠BDC = ∠CPD = 60&deg.

60°.