Олимпиадная задача по планиметрии: треугольник через треугольную дырку, 10-11 класс

  Достаточно доказать, что в треугольнике T найдётся высота h, меньшая наибольшей стороны треугольника Q.

  Пусть  a ≤ b ≤ c  – стороны треугольника Q. Так как его площадь равна 3, а наименьший угол A не превосходит 60°, то

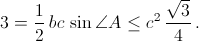  Отсюда  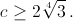   Аналогично получим, что наибольшая сторона треугольника T не меньше  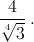   Значит, высота h, опущенная на эту сторону, не больше  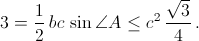   что и требовалось.

Ответ задачи отсутствует