Назад

Олимпиадная задача по планиметрии: пересечение прямых в трапеции (10–11 класс)

Задача 216162 • Сложность: 3 • 10-11 класс
Задача

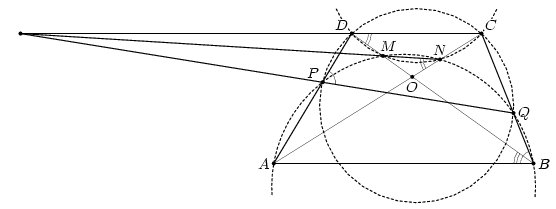
Дана неравнобокая трапеция ABCD  (AB || CD).  Окружность, проходящая через точки A и B, пересекает боковые стороны трапеции в точках P и Q, а диагонали – в точках M и N. Докажите, что прямые PQ, MN и CD пересекаются в одной точке.

Авторы:
Ивлев Ф.
Разделы:
Планиметрия
Источники:
Московская устная олимпиада по геометрии Олимпиады и турниры 09 (2011 год) 10-11 класс
Количество версий:
4
Решение

  Пусть O – точка пересечения диагоналей трапеции, а точки M и N лежат на отрезках DO и CO соответственно (см. рис.).

  Так как четырёхугольник APQB – вписанный, то  ∠DPQ = ∠ABC = 180° – ∠DCQ,  то есть DPQC – тоже вписанный. Aналогично из вписанности четырёхугольника AMNB следует вписанность четырёхугольника DMNC.

  Итак, есть три окружности, описанные около четырёхугольниковAPQB, DPQCиDMNC. PQ, MNиCD– их общие хорды, то есть каждая из этих прямых являетсярадикальной осьюпары соответствующих окружностей. Поэтому прямыеPQ, MNиCDпересекаются в одной точке –радикальном центреэтих окружностей.   Для другого расположения точекMиNдоказательство аналогично.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет