Олимпиадная задача по планиметрии: касательная к описанной окружности, 10–11 класс

Решение 1:Четырёхугольник ABDE – вписанный, поэтому  ∠CDE = ∠CAB.  Так как  C'D || CE,  то  ∠CAB = ∠DC'B,  а так как  C'E || CD,  то  ∠CDE = ∠C'ED.  Значит,  ∠C'ED = ∠DC'B,  откуда и следует утверждение задачи.

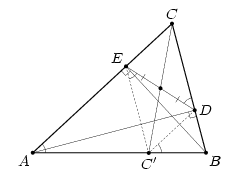
Решение 2:Пусть H – ортоцентр треугольника ABC, тогда точки D и E лежат на окружности с диаметром CH.

Kасательная к этой окружности в точкеCперпендикулярнаCH, то есть параллельнаAB. ТреугольникиDEC'иECDсимметричны относительно серединыDE, значит, симметричны и их описанные окружности, а также касательные, проведенные к этим окружностям в симметричных точкахC' иC. Так как центрально-симметричные прямые параллельны, то касательная в точкеC'к описанной окружности треугольникаDEC'совпадает с прямойAB.

Ответ задачи отсутствует