Олимпиадная задача по планиметрии: Стороны треугольников внутри друг друга

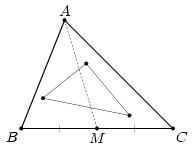
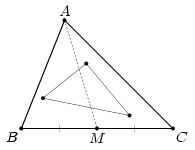
  Пусть   AB ≤ AC ≤ BC – стороны внешнего треугольника, M – середина стороны BC.   Первый способ. Заметим, что стороны треугольников ABM и ACM не превосходят AC.

  Действительно  BC < AB + AC ≤ 2AC,  то есть  BM = MC = ½ BC < AC.

  Кроме того, согласно задаче 155147  AM < AC.

  С другой стороны, хотя бы в одном из треугольников ABM или ACM лежат две вершины внутреннего треугольника (рис. слева). Значит, соединяющая их сторона не превосходит наибольшей стороны в этом треугольнике (см. задачу 157475 а), а, значит, не превосходит AC, и даже меньше неё, так как вершины внутреннего треугольника не совпадают с вершинами внешнего.

  Итак, хотя бы одна из сторон внутреннего треугольника меньше средней стороны внешнего, откуда и следует утверждение задачи.

  Второй способ. Проекции всех вершин внутреннего треугольника на прямую BC лежат внутри отрезка BC (рис. справа). Значит, проекция одной из его сторон меньше ½ BC. Проекция этой же стороны на перпендикулярную прямую меньше высоты внешнего треугольника, опущенной на BC. С другой стороны, проекция средней стороны внешнего треугольника на BC не меньше ½ BC, а на перпендикулярную прямую – равна высоте. Следовательно, одна из сторон внутреннего треугольника короче средней стороны внешнего.

Ответ задачи отсутствует