Олимпиадная задача по планиметрии: трапеция ABCD и перпендикуляры, 8-9 класс

  Пусть BC – меньшее основание трапеции. Из равенства сторон трапеции следует равенство углов:  ∠CAD = ∠CAB = ∠BCA = ∠DBC = ∠CDB = ∠BDA.

  Далее можно рассуждать по-разному:   Первый способ. Пусть M – основание перпендикуляра, опущенного из H на AC, а N – точка его пересечения с отрезком BD.

  Тогда  ∠MHC = 90° – ∠MCH = ∠CAH,  то есть четырёхугольник NHDC – вписанный. Следовательно,  ∠CND = ∠CHD = 90°,  то есть CN – высота равнобедренного треугольника BCD. Значит, N – середина BD.   Второй способ. Пусть N – середина BD, M — основание перпендикуляра, опущенного из N на AC, а H – точка его пересечения с отрезком D, K – точка пересечения CN и AD.   Точка N лежит на средней линии трапеции, следовательно,  CN = NK.  Учитывая, что  ∠NKH = 90°–∠BDA = 90° – ∠CAH = ∠NHK,  получим

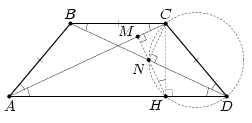
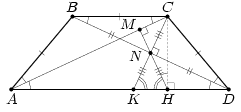
CN = NK = NH,  то есть  ∠CHK = 90°,  что и требовалось.   Третий способ. Пусть N и F – середины диагоналей BD и AC, прямая BF пересекает основание AD в точке E.

  Тогда  BF⊥AC,  то есть в треугольникеABEотрезокAFявляется высотой и биссектрисой. Следовательно,ABCE– ромб. ТреугольникECD– равнобедренный, следовательно,H– серединаED.  HN || BE⊥AC  как средняя линия треугольникаBDE.

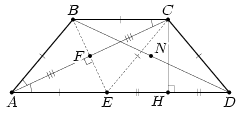
Ответ задачи отсутствует