Олимпиадная задача по планиметрии: отрезок MK и диагональ прямоугольника ABCD
Задача
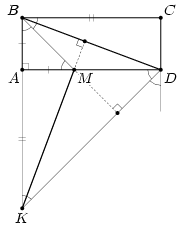
Биссектриса угла B и биссектриса внешнего угла D прямоугольника ABCD пересекают сторону AD и прямую AB в точках M и K соответственно.
Докажите, что отрезок MK равен и перпендикулярен диагонали прямоугольника.
Решение
Заметим, что ∠ABM = ∠AMB = ∠ADK = ∠AKD = 45° (см. рис.). Значит, AB = AM, AD = AK. Далее можно рассуждать по-разному.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет