Олимпиадная задача по планиметрии для 7–8 класса: равенство треугольников по высотам и медианам
Задача
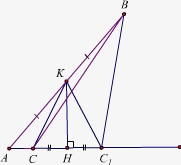
В треугольниках АВС и A1B1C1: ∠А = ∠А1, равны высоты, проведённые из вершин В и В1, а также равны медианы, проведённые из вершин С и С1. Обязательно ли эти треугольники равны?
Решение
Приведём пример двух неравных треугольников, для которых выполняются все равенства из условия задачи.
На одной из сторон острого угла A отложим произвольный отрезок AB (см. рис.). Из середины K отрезка AB опустим перпендикуляр KH на другую сторону угла. Отметим на этой стороне угла точки C и C1 так, чтобы HC = HC1. Тогда в треугольнике CKC1 совпадают высота и медиана, поэтому он – равнобедренный (KC = KC1).
Таким образом, в треугольниках ABC и ABC1 угол A – общий, высота, проведённая из вершины B – общая, и равны медианы CK и C1K, проведённые из вершин C и C1.
Ответ
Не обязательно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь