Олимпиадная задача по комбинаторной геометрии: максимальное число точек самопересечения ломаной с 7 звеньями
Задача
Какое наибольшее количество точек самопересечения может иметь замкнутая ломаная, в которой 7 звеньев?
Решение
Рассмотрим звено AB этой. На отрезке AB могут находиться не более четырёх точек самопересечения, поскольку со звеньями, исходящими из вершин A и B, отрезок AB пересечься не может. Так как у ломаной 7 звеньев и в каждой точке пересекаются два звена, то точек самопересечения не больше чем
7·4 : 2 = 14.
Пример ломаной, у которой 14 точек самопересечения, приведён на рисунке.
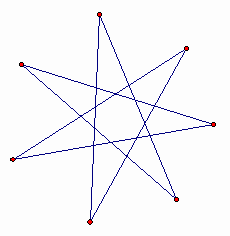
Ответ
14 точек.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет