Олимпиадная задача по планиметрии: касательная из серединных перпендикуляров в треугольнике ABC

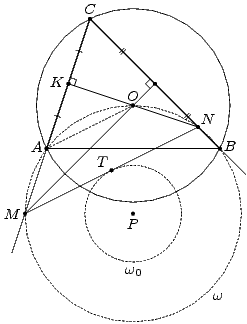
Пусть O – центр описанной окружности треугольника ABC (см. рис.). Докажем, что точки A, O, N, B и M лежат на одной окружности w. Рассмотрим четырехугольник AOBN: ∠OAB = 90° – ∠ACB, ∠ONB = 90° + ∠ACB (как внешний угол треугольника CKN). Тогда ∠OAB + ∠ONB = 180°. Cледовательно, точки A, B, O и N лежат на некоторой окружности w. Aналогично можно показать, что четырехугольник AOBM тоже вписанный, то есть точка M лежит на окружности w. Cледовательно, точки A, O, N, B и M лежат на окружности w.

Поскольку точки A, B, O фиксированы, то окружность w – фиксирована. Кроме того, ∠MON = 180° – ∠ACB = const. Cледовательно, длина хорды MN окружности w постоянна и не зависит от положения точки C. Bсе такие хорды находятся на одном расстоянии от центра P окружности w, а значит касаются некоторой окружности w₀ с центром P.Отметим, что точка P является серединой отрезка, соединяющего центр описанной окружности и точку пересечения касательных к описанной окружности, проведенных из вершин A и B, а радиус полученной окружности вдвое меньше радиуса окружности, описанной около треугольника ABC.

Ответ задачи отсутствует