Олимпиадная задача по планиметрии: построение перпендикуляра пятаком, 8–9 класс
Задача
На плоскости дана прямая. С помощью пятака постройте две точки какой-нибудь прямой, перпендикулярной данной. Разрешаются такие операции: отметить точку, приложить пятак к ней и обвести его; отметить две точки (на расстоянии меньше диаметра пятака), приложить пятак к ним и обвести его. Нет возможности прикладывать пятак к прямой так, чтобы она его касалась.
Решение
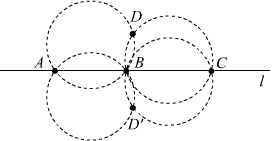
Отметим на данной прямой l три точки A, B и C так, чтобы AB и BC были меньше диаметра пятака. Прикладывая пятак к отрезкам AB и BC с одной стороны прямой, построим две окружности. Пусть они второй раз пересекутся в точке D. Прикладывая пятак к отрезкам AB и BC с другой стороны, получим две новые окружности, симметричные старым относительно l. Точка пересечения новых окружностей D' симметрична D относительно l, поэтому DD' ⊥ l.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь