Олимпиадная задача по многочленам и делимости: простота выражения x⁸ – x⁷y + ... + y⁸

x⁸ – x⁷y + x⁶y² – ... – xy⁷ + y⁸ = 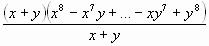   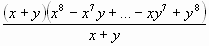=  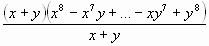  =     = (x² – xy + y²) (x⁶ – x³y³ + y⁶).

Полученные множители имеют одинаковый вид (неполный квадрат суммы). Но  a² – ab + b² = (a – b)² + ab ≥ 1,  если а и b – натуральные числа. Равенство возможно только при  x = y = 1,  тогда данное число равно 1, то есть не является простым. В остальных случаях каждый множитель больше 1, поэтому данное число – составное.

Ответ задачи отсутствует