Олимпиадная задача по планиметрии: биссектрисы в четырёхугольнике ABCD, 9-11 класс

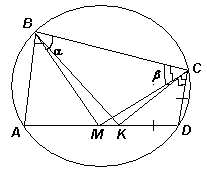
  Пусть M – точка пересечения биссектрис углов B и C.  Первый способ. Обозначим:  ∠ABC = 2α,  ∠ВСD = 2β,  тогда  ∠ADC = 180° – 2α,  ∠ВAD = 180° – 2β  (см. рис.).

  Пусть  α < β.  Выберем на луче DA такую точку K, что  DK = DС = 3,  тогда  ∠KCD = ∠CKD = α.  Следовательно, K лежит между М и D и

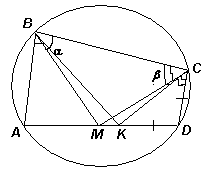
∠CKM + ∠CBM = 180°.  Значит, около четырёхугольника MKCВ можно описать окружность. Тогда  ∠KBM = ∠KCM = β – α,  значит,

∠ABK = β = ∠AKB,  следовательно,  AK = AB = 5,  AD = DK + AK = 8.

  Случай  α > β,  можно провести аналогичное рассуждение, откладывая на луче AD отрезок AK, равный АВ. Случай  α = β  невозможен, иначе ABCD – равнобокая трапеция  (AB = DC),  что противоречит условию.   Второй способ. Рассмотрим два случая.

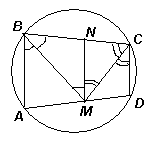
  1)  AB || DC.  Тогда ABCD – равнобокая трапеция  (ВС = AD,  см. рис.). Проведём  MN || AB.  Из равенства накрест лежащих углов получим:

BN = NM = NC,  значит, MN – средняя линия трапеции, то есть  MN = ½ (AB + DC).  Следовательно,  AD = BC = 2MN = AB + CD = 8.

  2) AB пересекает DC в точке T. Тогда M – либо центр вписанной окружности треугольника BTC, либо центр вневписанной окружности этого треугольника (см. рис.). Так как рассуждения в этих случаях полностью аналогичны, то рассмотрим только второй из них.   Пусть отрезок A'D' симметричен стороне AD относительно биссектрисы TM угла BTC. Тогда  ∠DA'M = ∠D'AM = ∠TCB:  так как ABCD – вписанный четырёхугольник, то  A'D' || BC.  Из равенства накрест лежащих углов получим, что  A'M' = A'C.  Аналогично, D'M = D'B,  кроме того,  AD' = A'D  (из симметрии). Таким образом,  AD = A'D' = A'M + D'M = A'C + D'B = AB + CD = 8.

AD = 8.