Олимпиадная задача по планиметрии и проективной геометрии, 8-11 класс, Богданов И. И.
Задача
Четырёхугольник ABCD описан около окружности, лучи BA и CD пересекаются в точке E, лучи BC и AD – в точке F. Вписанная окружность треугольника, образованного прямыми AB, CD и биссектрисой угла B, касается прямой AB в точке K, а вписанная окружность треугольника, образованного прямыми AD, BC и биссектрисой угла B, касается прямой BC в точке L. Докажите, что прямые KL, AC и EF пересекаются в одной точке.
Решение
Обозначим точки касания вписанной в четырёхугольник ABCD окружности со сторонами AB и BC через U и V. Имеем
равенство двойных отношений: 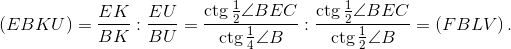
Отсюда следует, что прямые KL, EF, UV пересекаются в одной точке. Аналогично доказывается, что AC, EF, UV пересекаются в одной точке (см. рис.).
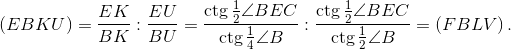
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь