Олимпиадная задача по планиметрии: Вписанные и вневписанные окружности треугольника, Белухов Н.

  Будем считать, что  AB > AC и, значит, точки B, N, M, C располагаются на прямой именно в таком порядке.   Лемма. Пусть K – середина BC, а I и J – центры вписанной и вневписанной окружностей. Тогда  AN || IK  и  AM || JK.

  Доказательство. Первое утверждение следует из того, что точка вписанной окружности, диаметрально противоположная M, лежит на прямой AN (поскольку вневписанная и вписанная окружность гомотетичны с центром в точке A), а K является также серединой MN (см. задачу 155404). Второе утверждение доказывается аналогично.   Из леммы видно, что условие задачи равносильно равенству  ∠IKJ = 180° – ½ ∠A. Покажем, что при  BC = 2MN  это выполнено. Действительно, в этом случае M и N будут серединами отрезков KC и KB, соответственно, IM и NJ являются серединными перпендикулярами к этим отрезкам. Значит, треугольники IKC и JKB равнобедренные (см. рис.), и  ∠JKB = 90° – ½ ∠B,  ∠IKC = ½ ∠C.

  Заметим, что точки B и C лежат на окружности с диаметром IJ. Её дуга BC соответствует углу  90° + ½∠A.  Когда хорда BC вращается внутри окружности, её середина K описывает концентрическую окружность меньшего радиуса. С другой стороны, геометрическое место таких точек K, что

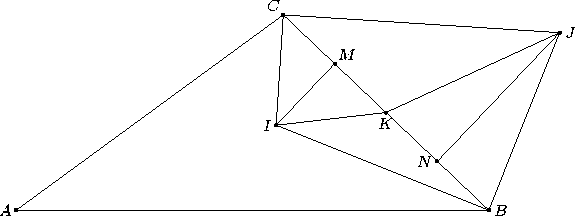
∠IKJ = 180° – ½ ∠A,  состоит из двух дуг с концами I и J. Эти два ГМТ пересекаются в четырёх точках, расположенных симметрично относительно отрезка IJ и серединного перпендикуляра к нему. Четыре четырёхугольника BICJ, соответствующие этим точкам, равны, то есть условие

∠IKJ = 180° – ½ ∠A  определяет четырёхугольник однозначно. Следовательно, оно равносильно равенству  BC = 2MN.

Ответ задачи отсутствует