Олимпиадная задача по планиметрии: биссектриса и медиана в треугольнике (8-11 класс)
Задача
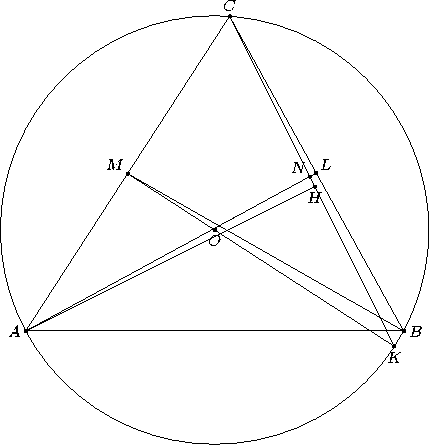
В треугольнике ABC ∠A = 57<°, ∠B = 61°, ∠C = 62°. Какой из двух отрезков длиннее: биссектриса угла A или медиана, проведённая из вершины B?
Решение
Пусть K – середина дуги ABC описанной окружности треугольника ABC, O – центр этой окружности; N – точка пересечения AL и CK, а AH – высота треугольника AKC (см. рис.). Так как ∠A < ∠C, то B лежит внутри дуги KC, значит, N лежит на отрезке AL, и AL > AN > AH. Далее можно рассуждать по-разному. Первый способ. AH > KM, так как это высоты меньшего и большего углов треугольника AKC. Следовательно, KM = MO + OK = MO + OB > MB.
Ответ
AL > BM.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет