Олимпиадная задача по планиметрии: построение четырёхугольника по радиусам и углу
Задача
Постройте четырёхугольник, в который можно вписать и около которого можно описать окружность, по радиусам этих окружностей и углу между диагоналями.
Решение
Если радиусы описанной и вписанной окружностей четырёхугольника равны R и r, а растояние между их центрами O и I равно d, то
= 
+ 
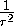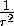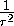(см. книгу И.Ф. Шарыгина «Задачи по геометрии. Планиметрия», 1986, задача II.248).
Значит, по данным R, r мы можем определить d и построить эти окружности. Как известно, диагонали всех четырёхугольников с данными описанной и вписанной окружностями пересекаются в одной и той же точке L, лежащей на прямой OI, а их середины лежат на окружности с диаметром OL. Кроме того, отрезок, соединяющий середины диагоналей, проходит через точку I (см. задачу 155451), а его длина равна OL sin φ, где φ – данный угол. Построив проходящую через I хорду такой длины, найдём середины диагоналей, а затем и вершины четырёхугольника.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь