Олимпиадная задача Френкина: Геометрическое место центров вписанных окружностей

  Если произвольный треугольник с вершинами на данных прямых перенести параллельно этим прямым, его центр вписанной окружности подвергнется такому же переносу. Следовательно, искомое ГМТ является полосой с краями, параллельным исходным прямым.

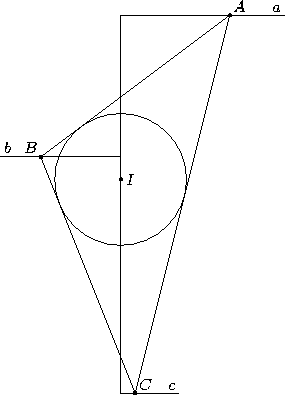
  Пусть a, c – крайние из исходных прямых, b – средняя, и на них соответственно находятся вершины треугольника A, C, B. Проведём диаметр вписанной окружности, перпендикулярный этим прямым, и рассмотрим его конец, ближайший к прямой a (см. рис.). Он лежит ближе к a, чем точка касания вписанной окружности со стороной AB , и, значит, ближе к a, чем прямая b. Так как другой конец диаметра находится ближе к a, чем прямая c, то середина диаметра лежит ближе к a, чем прямая, средняя между b и c. Поменяв в рассуждении местами a и c, получаем, что центр вписанной окружности I располагается в полосе, указанной в ответе.

  Возьмём теперь произвольный треугольник ABC с вершинами на соответствующих прямых. Переместим вершину B так, чтобы сторона AB стала перпендикулярна исходным прямым. Теперь устремим точку C в бесконечность. Углы при вершинах A и B стремятся к прямым, а точка I пересечения их биссектрис стремится к вершине равнобедренного прямоугольного треугольника с гипотенузой AB. Значит, I неограниченно приближается к прямой посредине между a и b. Аналогично, начав с того же треугольника, можно устремить I к прямой посредине между b и c. Следовательно, возможные положения I заполняют всю полосу, указанную в ответе.

Полоса, края которой не входят в ГМ, параллельны данным прямым и находятся посредине между средней прямой и крайними.