Олимпиадная задача по планиметрии Френкина: треугольник наибольшей площади
Задача
Даны окружность и не лежащая на ней точка. Из всех треугольников, одна вершина которых совпадает с данной точкой, а две другие лежат на окружности, выбран треугольник наибольшей площади. Докажите, что он равнобедренный.
Решение
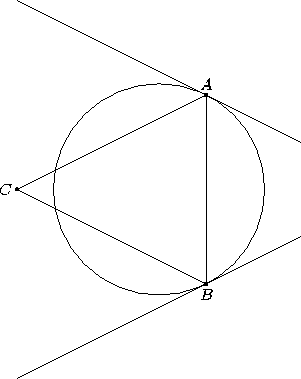
Пусть C – данная точка, A, B – точки на окружности (см. рис.). Если касательная к окружности в точке A не параллельна CB, то, переместив точку A, можно увеличить расстояние от неё до BC, а значит, и площадь треугольника. Аналогично касательная в точке B параллельна CA. Следовательно, прямые AC и BC симметричны относительно серединного перпендикуляра к AB, то есть AC = BC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет