Олимпиадная задача по планиметрии: площадь треугольника в конструкции с биссектрисой
Задача
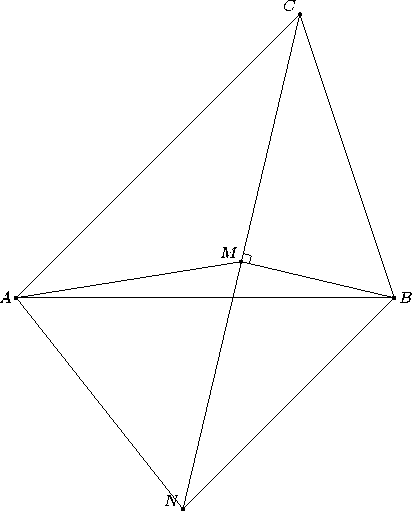
Дан треугольник ABC площади 1. Из вершины B опущен перпендикуляр BM на биссектрису угла C. Найдите площадь треугольника AMC.
Решение
Первый способ. Проведём через точку $B$ прямую, параллельную $AC$ до пересечения с биссектрисой угла $C$ в точке $N$ (см. рис.). Так как $\angle BNC = \angle ACN = \angle BCN$, то треугольник $BCN$ – равнобедренный и $BM$ – его медиана. Следовательно, $S_{AMC} = \frac12 S_{ANC} = \frac12 S_{ABC} = \frac12.$
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет