Олимпиадная задача по математике 8-11 классы: треугольник ABC и точки G, I, M

Олимпиадная задача по планиметрии и проективной геометрии для 8-11 классов: треугольник ABC и точки G, I, M

Задача

В треугольнике ABC M – точка пересечения медиан, I – центр вписанной окружности, A₁ и B₁ – точки касания этой окружности со сторонами BC и AC, G – точка пересечения прямых AA₁ и BB₁. Докажите, что угол CGI прямой тогда и только тогда, когда GM || AB.

Решение

Решение 1: Пусть C₁ – точка касания вписанной окружности со стороной AB, C₂ – вторая точка пересечения этой окружности с прямой CC₁. Тогда G лежит на отрезке CC₁. Существует центральная проекция, переводящая вписанную окружность в окружность, а G – в её центр. Треугольник ABC при этой проекции перейдёт в правильный, так что двойное отношение (CGC₁C₂) для любого треугольника такое же, как для правильного, то есть равно 3. Отсюда получаем цепочку равносильных утверждений: ∠CGI = 90°; G – середина C₁C₂; CC₁ = 3CC₂; CC₁ = 3GC₁; GM || AB.

Решение 2: Пусть AC₁ = x, BA₁ = y, CB₁ = z. По теореме Менелая 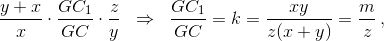где 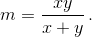Теперь, ∠IGC = 90° ⇔ CI² – r² = GC² – C₁G² ⇔ 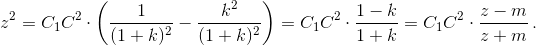Но, по теореме Стюарта (см. задачу 154717) 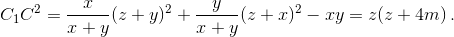Из этих двух равенств получаем, что 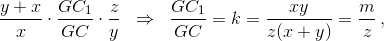⇔ z(z + m) = (z + 4m)(z – m) ⇔ 2zm = 4m² ⇔ z = 2m ⇔ k = ½, что и требовалось.