Олимпиадная задача Протасова на планиметрию: сравнение площадей треугольников
Задача
В угол A, равный α, вписана окружность, касающаяся его сторон в точках B и C. Прямая, касающаяся окружности в некоторой точке M, пересекает отрезки AB и AC в точках Р и Q соответственно. При каких α может быть выполнено неравенство SPAQ < SBMC?
Решение
Обозначим через I центр вписанной окружности треугольника PAQ. Имеем: ∠MCB = ∠MBP = ½ ∠ MPA = ∠IPQ. Аналогично ∠MBC = ∠IQP. Следовательно, треугольник IPQ подобен треугольнику MCB, откуда SIPQ/SMCB = (x/a)², где x = PQ, a = CB. C другой стороны, отношение SPAQ/SIPQ равно отношению периметра треугольника PAQ к стороне PQ, то есть 2b/x, где b = AB = AC (поскольку периметр треугольника PAQ равен 2b). Перемножая, получаем SPAQ/SMCB = 2bx/a². Отношение SPAQ/SMCB минимально, когда минимальна длина отрезка x = PQ.
Покажем, что наименьшее значение PQ достигается, когда треугольник APQ равнобедренный. Пусть O – центр окружности, вписанной в угол A; R – её радиус; M – середина дуги BC; M' – другая точка на этой дуге; PQ и P'Q' – отрезки соответствующих касательных между сторонами угла. Положим
β = ∠BOP = ∠POM = ∠MOQ = ∠COQ), γ = ∠BOP' = ∠P'OM', δ = ∠COQ' = ∠Q'OM'. Тогда PQ = PM + MQ = 2R tg β,
P'Q' = P'M' + M'Q' = R(tg γ + tg δ). Так как 2β = γ + δ и функция tg выпукла на интервале (0, π/2), то PQ < P'Q'.
Таким образом, достаточно рассмотреть случай, когда треугольник APQ – равнобедренный. Тогда a = 2b sin φ, где φ = α/2,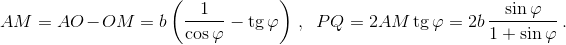 
Подставляя полученные выражения в неравенство 2bx/a² < 1, получаем: sin²φ + sin φ > 1.
Ответ
При 2 arcsin 
< α < π.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь