Олимпиадная задача: разрезание треугольника на три с равными радиусами описанных окружностей
Задача
Какие треугольники можно разрезать на три треугольника с равными радиусами описанных окружностей?
Решение
Если треугольник ABC остроугольный, то радиусы описанных окружностей треугольников ABH, BCH и CAH, где H – ортоцентр, равны (см. задачу 155597).
Пусть ∠C ≥ 90° и AC > BC. Возьмём на стороне AC такую точку D, что AD = BD, а на стороне AB такую точку E, что ∠AED = ∠C (это возможно, так как ∠A < 180° – ∠C). По теореме синусов радиусы описанных окружностей треугольников ADE, BDE и BDC равны (см. рис.).
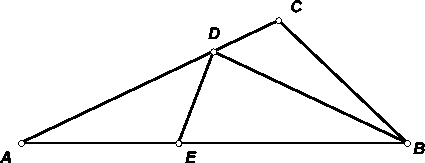
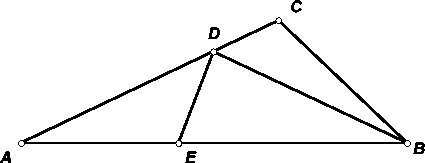
Ответ
Все, кроме равнобедренных неостроугольных.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет