Олимпиадная задача по планиметрии и проективной геометрии Протасова для 8–11 классов
Задача
На сторонах угла взяты точки A, B. Через середину M отрезка AB проведены две прямые, одна из которых пересекает стороны угла в точках A1, B1, другая – в точках A2 , B2. Прямые A1B2 и A2B1 пересекают AB в точках P и Q. Докажите, что M – середина PQ.
Решение
Решение 1: Пусть C – вершина данного угла (см. рис.). Применив теорему Менелая (см. задачу 153857) к треугольнику ABC и прямой A2B2, получим
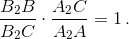Аналогично,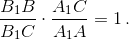 
Применив теорему Менелая к треугольнику ABC и прямой A1B2, получим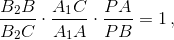 
откуда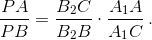 
Аналогично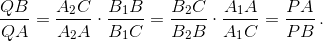 
Следовательно, PA = QB, что и требовалось.
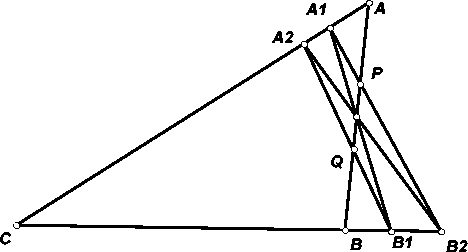
Решение 2: Сделаем центральную симметрию относительно точки M. Пусть точки A1 и B2 переходят в точки A3 и B3 соответственно. Надо доказать, что прямые AB, A2B1 и B3A3 пересекаются в одной точке. Далее можно рассуждать по-разному. Первый способ. Проведём через точку M прямую, параллельную BC. Из подобия треугольников следует, что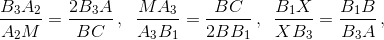 
где X – точка пересечения прямых AB и B1B3. Перемножив, получаем 
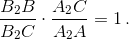Из теоремы Чевы (см. задачу 153856), примененной к треугольнику MB1B2, следует, что прямые MX, B1A2 и B3A3 пересекаются в одной точке, что и требовалось. Второй способ. Прямые AA2 и BB1, пересекаются в точке C; прямые A2B3 и B1A3, совпадающие соответственно с A2B2 и B1A1, пересекаются в точке M. Прямые AB3 и BA, симметричные соответственно BB2 и AA1, пересекаются в точке C1, симметричной точке C. Точки C, M и C1 лежат на одной прямой, поэтому из теоремы, обратной к теореме Дезарга, применённой к треугольникам AA2B3 и BB1A3, следует, что прямые AB, A2B1 и B3A3 пересекаются в одной точке.
Решение 3: Рассматривая центральные проекции прямой AB на прямую AC из точек B1, B2, получаем равенство двойных отношений (см. рис.)
(APMB) = (AA1A2C) = (CA2A1A) = (BQMA), что равносильно утверждению задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь