Олимпиадная задача по планиметрии: равенство углов в треугольнике ABC
Задача
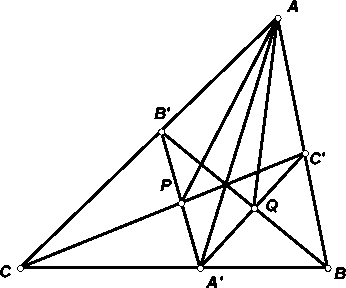
В треугольнике ABC проведены биссектрисы AA', BB' и CC'. Пусть P – точка пересечения A'B' и CC', а Q – точка пересечения A'C' и BB'.
Докажите, что ∠PAC = ∠QAB.
Решение
Применяя теорему синусов к треугольникам AC'Q и AA'Q, получаем (см. рис.)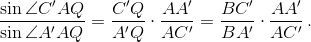 
Аналогично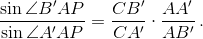 
Потеореме Чевы(см. задачу153856) эти отношения равны, что равносильно утверждению задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет