Олимпиадная задача по планиметрии для 8–11 классов от Заславского А. А.
Задача
В трапеции ABCD с основаниями AD и BC P и Q – середины диагоналей AC и BD соответственно. Докажите, что если ∠DAQ = ∠CAB, то ∠PBA = ∠DBC.
Решение
Решение 1:Пусть K – точка пересечения диагоналей трапеции. Применяя теорему синусов к треугольникам AQD, AQB, ALD, ALB, получим, что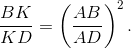 
Следовательно, 
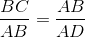и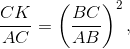 
что, как показано выше, равносильно утверждению задачи.
Решение 2:Пусть L и M – середины соответственно AB и AD. Тогда, так как PL || AD, QM || AB, то ∠AQM = ∠QAB = ∠CAD = ∠APL, и значит, треугольники APL и AMQ подобны (см. рис.). Следовательно, AP : AQ = AL : AM = AB : AD. Поэтому треугольники ABP и ADQ подобны, то есть ∠ABP = ∠ ADQ = ∠CBD.
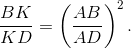
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет