Олимпиадная задача по планиметрии для 8–11 классов от Заславского А. А.

Задача

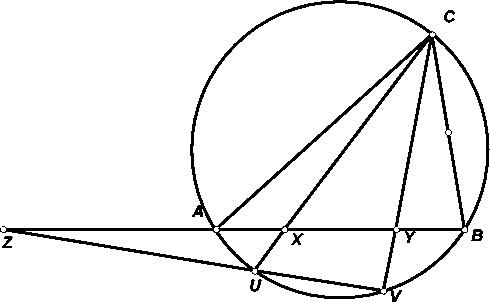
На стороне AB треугольника ABC взяты такие точки X, Y, что AX = BY. Прямые CX и CY вторично пересекают описанную окружность треугольника в точках U и V. Докажите, что все прямые UV проходят через одну точку.

Решение

Решение 1: Пусть Z – точка пересечения AB и UV. Применяя теорему синусов к треугольникам ZAU и ZBV, получаем (см. рис.)

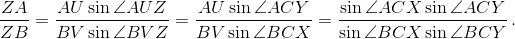Из треугольникаACXимеем: sin∠ACX = ^AX/_ACsin∠AXC. Из этого и трёх аналогичных соотношений получаем, что ZA:ZB = BC² :AC², то есть не зависит от выбора точекX, Y.

Решение 2: Точка C', симметричная C относительно серединного перпендикуляра к отрезку AB, лежит на описанной окружности треугольника ABC. Пусть касательная в этой точке пересекает AB в точке Z. Проведём через Z произвольную секущую к окружности, пересекающую её в точках U, V, и найдём точки X, Y пересечения прямых CU, CV с AB. Имеем: 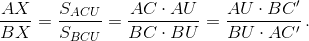Аналогично 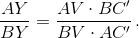Перемножая эти равенства, получаем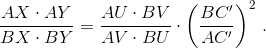

Из подобия треугольников ZAU и ZVB следует, что 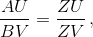а из подобия треугольников ZAV и ZUB – AV : BU = ZV : ZB. Кроме того, ZU·ZV = ZC'². Следовательно, 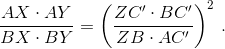Из подобия треугольников ZAC' и ZC'B получаем, что правая часть этого соотношения равна 1. Значит, AX = BY и точка Z является общей точкой прямых из условия задачи.