Геометрическое место центров треугольников через три точки: олимпиадная задача планиметрии
Задача
Найдите геометрическое место центров правильных треугольников, стороны которых проходят через три заданные точки A, B, C (то есть на каждой стороне или ее продолжении лежит ровно одна из заданных точек).
Решение
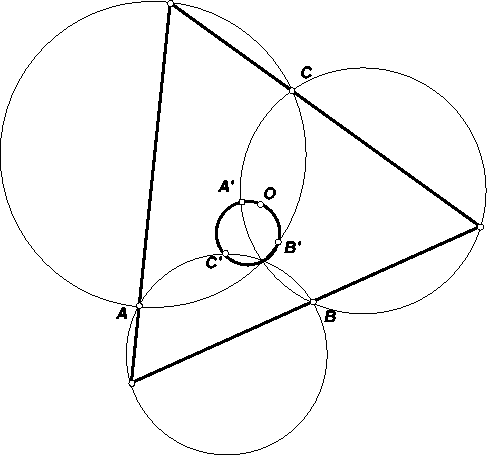
Построим на сторонах треугольника ABC во внешнюю сторону дуги, вмещающие угол 60°, и найдём середины A', B', C' дополнительных дуг. Прямые, соединяющие центр треугольника с его вершинами, проходят через A', B', C', а поскольку вершины двигаются по построенным окружностям с равными угловыми скоростями, углы, под которыми из центра видны отрезки A'B', B'C', C'A', остаются постоянными. Следовательно, искомое ГМТ – окружность A'B'C' (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет