Олимпиадная задача: Равенство треугольников в планиметрии (Заславский А. А.)
Задача
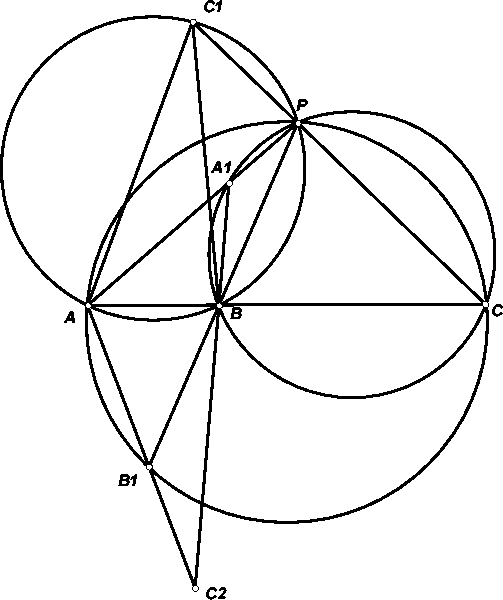
Три окружности проходят через точку P, а вторые точки их пересечения A, B, C лежат на одной прямой. A1, B1, C1 – вторые точки пересечения прямых AP, BP, CP с соответствующими окружностями. C2 – точка пересечения прямых AB1 и BA1. A2, B2 определяются аналогично.
Докажите, что треугольники A1B1C1 и A2B2C2 равны.
Решение
Так как четырёхугольники PAB1C и PBAC1 вписанные, ∠CAC2 = ∠CAB1 = ∠CPB1 = ∠BAC1 (см. рис.). Аналогично ∠ABC2 = ∠ABC1, то есть точки C1, C2 симметричны относительно прямой AB. Повторив это рассуждение для двух других пар точек, получим, что треугольники A1B1C1 и A2B2C2 симметричны относительно этой прямой и, следовательно, равны.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет