Олимпиадная задача по планиметрии и комбинаторной геометрии от Френкина Б. Р.: разбиение выпуклого n-угольника на равные треугольники
Задача
Отрезки, соединяющие внутреннюю точку выпуклого неравностороннего n-угольника с его вершинами, делят n-угольник на n равных треугольников.
При каком наименьшем n это возможно?
Решение
Докажем, что при n = 3, 4 указанная ситуация невозможна. Первый способ. При n = 3 углы треугольников разбиения, сходящиеся во внутренней точке, равны, так как сумма любых двух разных углов в них меньше 180°. Но тогда равны и противолежащие им стороны, являющиеся сторонами многоугольника. Противоречие.
Пусть четырёхугольник ABCD разрезан на равные треугольники отрезками, проведёнными из точки O. Проведём ломаную (или прямую) AOC. В точке O сумма двух углов, находящихся с некоторой стороны от AOC, не меньше 180°. Аналогично случаю n = 3 получаем, что соответствующие стороны равны. Рассмотрев ломаную BOD, получаем равенство одной из этих сторон и третьей стороны. Пусть, скажем, AB = BC = CD = l.
Предположим, что AD ≠ l. В треугольнике AOD есть сторона длины l, скажем AO. Таким образом, в треугольнике AOB (и всех равных ему) имеется две стороны длины l. Как следствие, AO = DO = l. В треугольнике BOC имеется две стороны длины l. Одна из них BC, а другая, скажем, BO. Но тогда в треугольнике AOB все стороны равны. Следовательно, это верно и для треугольника AOD, то есть AD = l. Противоречие. Второй способ. Так как треугольники, на которые разрезается данный треугольник равны, то равны радиусы описанных около них окружностей и площади. Из первого следует, что точка, определяющая разрезание, является ортоцентром треугольника (см. задачу 156681 а), а из второго, что она является точкой пересечения его медиан (см. задачу 154992). Но ортоцентр и точка пересечения медиан совпадают только в правильном треугольнике (см. задачу 208458).
∠OAB = ∠OCB, как углы, противоположные одной и той же стороне равных треугольников. Аналогично, ∠OAD = ∠OCD, ∠OBC = ∠ODC,
∠OBA = ∠ODA. Следовательно, ∠A = ∠C, ∠B = ∠D, и ABCD – параллелограмм. Так как отрезки из O делят его на равновеликие треугольники, O – точка пересечения его диагоналей, а тогда из равенства треугольников следует, что ABCD – ромб. При n = 5 указанная ситуация возможна (см. рис.).
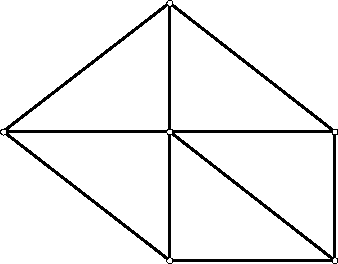
Ответ
n = 5.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь