Олимпиадная задача Сергеева: свойства функции на векторах — Алгебра и стереометрия, 10-11 класс

  Оценка. Последовательно докажем, что описанная в условии функция  f принимает:

  а) не более двух различных значений на любой прямой (проходящей через точку O): действительно, если она на трёх векторах одной прямой принимает разные значения, причём на векторе v – наибольшее, а на некотором ненулевом (такой найдётся) векторе u – меньшее значение, то для некоторого числа α получим противоречие:  v = αu  ⇒   f(v) = f(αu + 0·u) ≤ f(u);

  б) не более трёх различных значений на любой плоскости (проходящей через точку O): действительно, если она на четырёх векторах одной плоскости принимает разные значения, причём на векторе v – наибольшее, а на некоторых неколлинеарных (такие, в силу предыдущего пункта, найдутся) векторах u₁, u₂ – меньшие значения, то для некоторых чисел α₁, α₂ получим противоречие:  v = α₁u₁ + α₂u₂  ⇒  f(v) = f(α₁u₁ + α₂u₂) ≤ max{f(u₁), f(u₂)};

  в) не более четырёх различных значений на всём пространстве: действительно, если она на пяти векторах принимает разные значения, причём на векторе v – наибольшее, а на некоторых некомпланарных (такие, в силу предыдущего пункта, найдутся) векторах u₁, u₂, u₃ – меньшие значения, то для некоторых чисел α₁, α₂, α₃ получим противоречие:

    v = α₁u₁ + α₂u₂ + α₃u₃  ⇒  f(v) = f(α₁u₁ + (α₂u₂ + α₃u₃)) ≤ max{f(u₁), f(α₂u₂ + α₃u₃)} ≤ max{f(u₁), max{f(u₂), f(u₃)}} = max{f(u₁), f(u₂), f(u₃)}.   Пример функции f, удовлетворяющей условию задачи и принимающей ровно четыре различных значения: введя в пространстве декартовы координаты с началом в точке O, определим  v = (x, y, z),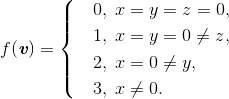  

Ответ задачи отсутствует