Олимпиадная задача по планиметрии: центры окружностей и точки треугольника
Задача
В треугольнике АВС : АС =
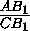 . Докажите, что центры вписанной и описанной
окружностей треугольника АВС , середины сторон АВ и ВС и
вершина В лежат на одной окружности.
. Докажите, что центры вписанной и описанной
окружностей треугольника АВС , середины сторон АВ и ВС и
вершина В лежат на одной окружности.
Решение
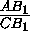
Пусть О — центр окружности, описанной
около треугольника АВС , С1 и А1 — середины сторон АВ и ВС соответственно, тогда ОС1 и ОА1 — серединные
перпендикуляры к этим сторонам (см. рис.). Так как отрезок ОВ виден из точек С1 и А1 под углом90o , то эти
точки лежат на окружности с диаметром ОВ .
Таким образом, мы доказали, что четыре из пяти указанных в условии
задачи точек лежат на одной окружности, не используя условия АС
=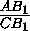 . Покажем теперь, что если это условие
выполняется, то на рассматриваемой окружности лежит также и точка I — центр окружности, вписанной в треугольник АВС .
Это можно сделать различными способами.
Первый способ.
. Покажем теперь, что если это условие
выполняется, то на рассматриваемой окружности лежит также и точка I — центр окружности, вписанной в треугольник АВС .
Это можно сделать различными способами.
Первый способ.
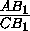
Пусть ВВ1 — биссектриса
треугольника АВС , тогда 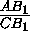 =
=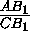 =
=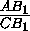 (см.
рис.). Учитывая, что АС =
(см.
рис.). Учитывая, что АС = 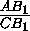 +
+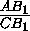 =
AC1+CA1 , получим, что AC1=AB1 и CA1=CB1 .
Поскольку AI — биссектриса
угла А , то она совпадает с высотой и медианой равнобедренного
треугольника AB1C1 , поэтому, треугольник IB1C1 также
равнобедренный, то есть IC1=IB1 . Аналогично доказывается, что IA1=IB1 . Следовательно, IC1=IA1 .
Таким образом, в треугольниках BIC1 и BIA1 : BI — общая сторона,
=
AC1+CA1 , получим, что AC1=AB1 и CA1=CB1 .
Поскольку AI — биссектриса
угла А , то она совпадает с высотой и медианой равнобедренного
треугольника AB1C1 , поэтому, треугольник IB1C1 также
равнобедренный, то есть IC1=IB1 . Аналогично доказывается, что IA1=IB1 . Следовательно, IC1=IA1 .
Таким образом, в треугольниках BIC1 и BIA1 : BI — общая сторона,  С1BI =
С1BI =
 A1BI , IC1=IA1 . Следовательно,
A1BI , IC1=IA1 . Следовательно,  BC1I=
BC1I= BA1I или
BA1I или  BC1I+
BC1I+ BA1I=180o
(Это следует, например, из решения
задачи на построение треугольника по двум сторонам и углу,
противолежащему одной из этих сторон, или из теоремы
синусов, примененной к рассматриваемым
треугольникам:
BA1I=180o
(Это следует, например, из решения
задачи на построение треугольника по двум сторонам и углу,
противолежащему одной из этих сторон, или из теоремы
синусов, примененной к рассматриваемым
треугольникам: 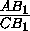 =
=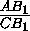 =
=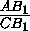 =
=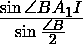 , откуда sin
, откуда sin BC1I= sin
BC1I= sin BA1I .).
Первый случай реализуется, если ВС1 = ВА1 , то есть треугольник АВС — равносторонний. Тогда центры его описанной и вписанной
окружностей совпадают. Во втором случае четырехугольник BC1IA1 является вписанным, что и требовалось.
Второй способ.
BA1I .).
Первый случай реализуется, если ВС1 = ВА1 , то есть треугольник АВС — равносторонний. Тогда центры его описанной и вписанной
окружностей совпадают. Во втором случае четырехугольник BC1IA1 является вписанным, что и требовалось.
Второй способ.
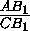
Докажем сначала, что в данном треугольнике центр I вписанной окружности делит пополам отрезок BB2 , где точка B2 — вторая точка пересечения прямой BI c окружностью, описанной около
треугольника АВС (см. рис.).
Используем равенство B2A=B2I=B2C , справедливое для любого
треугольника (), из которого следует, что B2 — центр окружности радиуса R ,
описанной около треугольника AIC . По следствию из теоремы синусов для этого треугольника,
учитывая, что угол AIC между биссектрисами треугольника АВС равен90o + 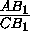 , получим: B2I=R=
, получим: B2I=R=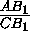 =
=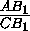 .
Кроме того, если окружность, вписанная в треугольник АВС ,
касается стороны АВ в точке C2 , то BC2=
.
Кроме того, если окружность, вписанная в треугольник АВС ,
касается стороны АВ в точке C2 , то BC2=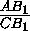 . Учитывая, что АС =
. Учитывая, что АС =
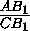 , получим: BC2=
, получим: BC2=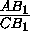 . Тогда, из прямоугольного треугольника BC2I получим, что BI=
. Тогда, из прямоугольного треугольника BC2I получим, что BI=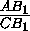 .
Таким образом, доказано, что B2I=BI .
.
Таким образом, доказано, что B2I=BI .
Теперь
заметим, что при гомотетии с центром В и коэффициентом2образом рассмотренного ранее
треугольника BC1A1 является данный треугольник ВСА (см. рис.). Это означает, что при
указанной гомотетии центр окружности, вписанной в треугольник BC1A1 , переходит в центр
окружности, вписанной в треугольник АВС . По доказанному выше, BI1=II1 (так как треугольник BC1A1 подобен треугольнику ВСА , то для него также выполняется соотношение A1C1=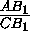 (BC1+BA1)), то точка I лежит на окружности, описанной около треугольника BC1A1 , что и требовалось.
Это утверждение, называемое "теоремой трилистника", можно
доказать, например, так (см. рис.10.6в): B2A = B2C , так
как эти хорды стягивают равные дуги окружности; B2A = B2I , так как
(BC1+BA1)), то точка I лежит на окружности, описанной около треугольника BC1A1 , что и требовалось.
Это утверждение, называемое "теоремой трилистника", можно
доказать, например, так (см. рис.10.6в): B2A = B2C , так
как эти хорды стягивают равные дуги окружности; B2A = B2I , так как  AIB2=
AIB2= B2AI=
B2AI=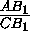 (
( A+
A+ B).
B).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь