Олимпиадная задача по планиметрии: построение треугольника с равной площадью, 8–10 класс

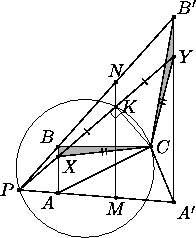
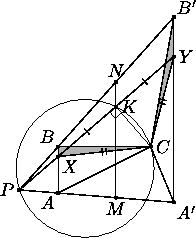
  Если треугольники ABC и A₁B₁C₁ равны, то способ построения очевиден. В противном случае можно считать, что  AB ≠ A₁B₁  (пусть для определенности  AB < A₁B₁).

  Построим такой треугольникA'B'C, что  AB || A'B', A'B' = A₁B₁, B'C = B₁C₁, CA' = C₁A₁(см. рис.; это построение легко осуществить, например, используя равенство  ∠BCB'= ∠B+ ∠B₁).   ТогдаABB'A'– трапеция. ПустьMN– её средняя линия, аP– точка пересечения продолжений боковых сторон. Построим на отрезкеPC, как на диаметре, окружность ω. Так как  AB < A₁B₁=A'B', S_ABC = S_A1B1C1=S_A'B'C,  то расстояние от точкиCдо прямойABбольше расстояния отCдо прямойA'B', поэтому точкиPиCлежат по разные стороны от прямойMN, следовательно, ω пересекает прямуюMN. ПустьK– одна из точек пересечения (на рисунке она лежит на отрезкеMN, но наши рассуждения на это опираться не будут).   Проведём прямуюPKдо пересечения с прямымиABиA'B'в точкахXиYсоответственно. Тогда  AX:XB = A'Y:YB',  поэтому  S_XBC = S_YB'C.  Кроме того,  XK = KY,  а уголPKC– прямой как опирающийся на диаметр в окружности ω. Значит,CK– серединный перпендикуляр к отрезкуXY, и  CX = CY.   На продолжении отрезкаXCза точкуCвозьмём такую точкуZ, что  XC = CZ.  Построим треугольникиA₂CZиB₂CZ, равные треугольникамA'CYиB'CYсоответственно. Тогда треугольникиA₂B₂C, A'B'CиA₁B₁C₁. Покажем, что  AA₂||BB₂  (тогда можно сдвинуть треугольникA₂B₂Cвдоль прямойAA₂, получив требуемый). Так как  CX = CZ,  S_ABC = S_A2B2C  и  S_XBC = S_ZB2C, то  S_XAC = S_ZA2C,  расстояния от точекAиA₂до прямойXZравны, и расстояния от точекBиB₂до прямойXZтакже равны. Следовательно,  AA₂||XZ || BB₂,  что и требовалось.

Ответ задачи отсутствует