Олимпиадная задача по планиметрии: биссектрисы и окружности в треугольнике ABC
Задача
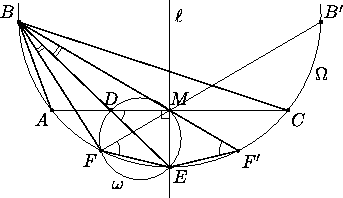
В треугольнике ABC проведена биссектриса BD (точка D лежит на отрезке AC ). Прямая BD пересекает окружность Ω , описанную около треугольника ABC , в точках B и E . Окружность ω , построенная на отрезке DE как на диаметре, пересекает окружность Ω в точках E и F . Докажите, что прямая, симметричная прямой BF относительно прямой BD , содержит медиану треугольника ABC .
Решение
Пусть M — середина стороны AC , прямая BM пересекает окружность Ω вторично в точке F' , а прямая FM пересекает окружность Ω вторично в точке B' . Так как 
ABE = CBE , то E — середина дуги AC , поэтому M и E лежат на серединном перпендикуляре 
к отрезку AC . Значит, EMD=90o и, следовательно, M лежит на окружности ω . Имеем: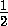 
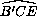= B'FE =
MFE = MDE = CDE = (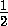
+ 
)= ( + 
) = 
.
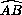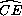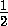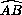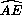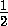
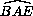Из равенства дуг B'CE и BAE следует, что точки B и B' симметричны относительно , поэтому прямые BM и B'M (а стало быть,
и точки F' и F ) симметричны относительно . Последнее утверждение означает, что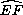 
= 
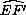, откуда FBE = F'BE .
Получаем, что прямые BF и BM симметричны относительно прямой BE , что и требовалось доказать.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь