Олимпиадная задача по математике: сколько раз функция меняет знак на отрезке [0, 2009π/2]

  Обозначим  n = 2009.  Рассмотрим функцию  cos ^π/k.  Она меняет знак при  x = k(πm + ^π/₂) = ^k(2m+1)π/₂,  где m – произвольное целое число. Значит, нулями функции  f(x) могут являться только точки  x_i = ^πi/₂,  где  1 ≤ i ≤ n.  Тогда менять знак она может лишь в точках x_i при  i = 1, 2, ..., n – 1.

  Функция  cos ^x/_k  меняет знак в точке x_i, если  i = k(2m + 1)  при целом m. Значит, количество косинусов, которые меняют знак в точке x_i, совпадает с количеством нечётных делителей числа i. Поэтому функция  f(x) будет менять знак в тех и только тех точках  x_i, для которых у числа i нечётное количество нечётных делителей. Пусть  i = 2^lj,  где l целое, а j нечётно. Тогда количество нечётных делителей у чисел i и j совпадает. Но у нечётного числа  j количество делителей нечётно тогда и только тогда, когда  j – точный квадрат (см. задачу 130365).

  В итоге получаем, что функция  f(x) меняет знак в точке x_i, если число i – либо квадрат, либо удвоенный квадрат (в зависимости от чётности числа l). Но среди чисел от 1 до  n – 1  есть 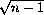 []  квадратов, и  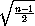[]  удвоенных квадратов. Значит, количество перемен знака равно

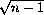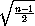[] + [] = 44 + 31 = 75.

Ответ задачи отсутствует