Олимпиадная задача по планиметрии: параллелограмм и точки пересечения (Емельянов Л. А.)

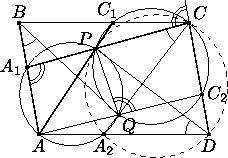
Обозначим описанные окружности треугольников  AA₁P и  CC₁P через  ω_A и  ω_C , соответственно. Пусть лучи AQ и CQ пересекают стороны  CD и  AD в точках  C₂ и  A₂ соответственно. Тогда из параллельности AB|| CD и вписанности четырехугольника  AA₁PQ получаем PCC₂=180^o- AA₁P= AQP=180^o- PQC₂ , то есть четырехугольник  CPQC₂ также вписан. Это значит, что C₂ лежит на  ω_C ; аналогично, точка  A₂ лежит на  ω_A рисунке. Далее, так как четырехугольник AA₁PA₂ вписан и AB|| CD , имеем A₂PC=180^o- A₁PA₂= A₁AA₂=180^o- A₂DC , то есть четырехугольник  A₂PCD также вписан. Тогда PDA= PDA₂= PCA₂= PCQ . Аналогично получаем, что четырехугольник  BA₁QC вписан, откуда QBA= QCA₁= PCQ . Отсюда следует PDA= PCQ= QBA , что и требовалось доказать. Утверждение задачи остается верным, если Q не лежит в треугольнике  ACD .

Ответ задачи отсутствует