Олимпиадная задача по логарифмам и рациональным функциям для 11 класса (Терешин Д. А.)
Задача
Пусть1<a b
b c . Докажите, что
c . Докажите, что
log a b+log b c+log c a log b a+log c b+log a c.
log b a+log c b+log a c.
Решение
Введем переменные x=log a b , y=log b c . В новых переменных неравенство принимает вид
x+y+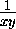

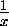 +
+ +xy,
+xy,
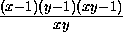
 0.
0.
 1, y
1, y 1и xy
1и xy 1в силу условия задачи.
1в силу условия задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет