Олимпиадная задача по стереометрии и планиметрии: свойства треугольной пирамиды, 10-11 класс

Пусть AB₁ , AC₁ , AD₁  — высоты граней ACD , ABD , ABC . Точки пересечения высот этих граней лежат на прямых  AB₁ , AC₁ , AD₁ и отличны от точки  A . Поскольку они лежат на одной прямой 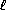 , то прямые  AB₁ , AC₁ , AD₁ лежат в плоскости  α , содержащей 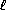 и  A (ясно, что  A не лежит на  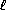). Значит, точки  B₁ , C₁ , D₁ лежат на прямой пересечения плоскостей  α и  BCD .

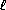
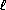
Пусть  A'  – проекция точки  A на плоскость  BCD . Тогда по теореме о трех перпендикулярах точки  B₁ , C₁ , D₁ являются проекциями  A' на прямые  CD , BD , BC . Значит, точки  A' , C , B₁ , D₁ лежат на одной окружности (с диаметром  A'C ), а также точки  A' , D , B₁ , C₁ лежат на одной окружности (с диаметром  A'D ). Отсюда 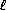(BC,A'C) = 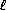(D₁C,A'C) = 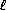(D₁B₁,A'B₁) = 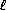(C₁B₁,A'B₁) = 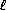(C₁D,A'D) = 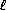(BD,A'D)(здесь через 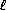(a, b)обозначен угол от прямой a до прямой b , отсчитываемый против часовой стрелки; этот угол считается с точностью до прибавления числа вида π k , где k — целое). Из равенства 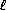(BC,A'C) = 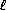(BD,A'D)следует, что точка  A' лежит на описанной окружности треугольника  BCD и, следовательно, на описанной сфере  S пирамиды  ABCD . Тогда центр  O сферы  S лежит в плоскости  β , являющейся серединным перпендикуляром к  AA' . Ясно, что середины ребер  AB , AC , AD также лежат в  β (так как треугольники ABA' , ACA' , ADA' прямоугольные). Это и требовалось доказать. Замечание 1.Опустим перпендикуляры из произвольной точки  A' , лежащей в плоскости  BCD , на прямые BC , CD , BD . Их основания лежат на одной прямой тогда и только тогда, когда A' лежит на описанной окружности треугольника  BCD . Эта прямая называется прямой Симсона точки  A' . Замечание 2.Тетраэдры, удовлетворяющие условию задачи, существуют.

Ответ задачи отсутствует