Олимпиадная задача по математике: перпендикуляры к касательной, 8-9 класс

Олимпиадная задача по планиметрии: касательная, окружность и перпендикуляры, 8-9 класс

Задача

Пусть точки A , B , C лежат на окружности, а прямая b касается этой окружности в точке B . Из точки P , лежащей на прямой b , опущены перпендикуляры PA₁ и PC₁ на прямые AB и BC соответственно (точки A₁ и C₁ лежат на отрезках AB и BC ). Докажите, что A₁C₁ 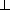AC .

Решение

Поскольку PC₁B = PA₁B = 90^o , четырёхугольник PA₁C₁B вписан. Значит, CC₁A₁ = 180^o - A₁C₁B = A₁PB = 90^o - A₁BP . С другой стороны, A₁BP = ACB = 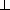AB . Поэтому CC₁A₁ = A₁PB = 90^o - ACC₁ , то есть прямые A₁C₁ и AC пересекаются под прямым углом.