Олимпиадная задача по планиметрии: деление ломаных через точку на окружности
Задача
Прямые, касающиеся окружности ω в точках B и D, пересекаются в точке P. Прямая, проходящая через P, высекает на окружности хорду AC. Через точку отрезка AC проведена прямая, параллельная BD. Докажите, что она делит длины ломаных ABC и ADC в одинаковых отношениях.
Решение
Треугольники PBA и PCB подобны, так как угол BPC – общий, а ∠PBA = ∠PCB. Значит, BA : BC = PB : PC. Аналогично DA : DC = PD : PC. Так как PB = PD, то BA : BC = DA : DC, или AB : AD = CB : CD. Отсюда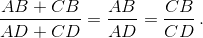 
Обозначим через Q точку пересечения отрезков AC и BD. Пусть для определенности точка T лежит на отрезке QC, а прямая, проходящая через T параллельно BD, пересекает CB и CD в точках B' и D', соответственно. Тогда по теореме Фалеса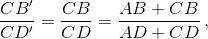 
или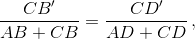 
что и требовалось.
Если же точка T лежит на отрезке AQ, то аналогично рассматриваются отрезки, высекаемые на сторонах AB и AD.
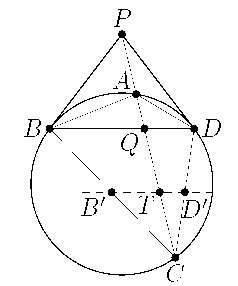
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь