Олимпиадная задача по планиметрии: вписанный четырехугольник и перпендикулярные углы, 8-9 класс
Задача
Четырёхугольник ABCD вписан в окружность с диаметром AC. Точки K и M – проекции вершин A и C соответственно на прямую BD. Через точку K проведена прямая, параллельная BC и пересекающая AC в точке P. Докажите, что угол KPM – прямой.
Решение
Обозначим через E точку пересечения диагоналей AC и BD. Пусть для определенности точка K лежит на отрезке BE. Первый способ. Пусть прямая, проходящая через K параллельно PM, пересекает AC в точке N (рис. слева). Треугольник NKE и PME подобны (так как их стороны параллельны), откуда PE : EM = NE : EK. Прямоугольные треугольники AKE и CME также подобны, поэтому EM : EC = EK : EA. Перемножая полученные равенства, получаем PE : EC = NE : EA. Но по теореме Фалеса PE : EC = KE : EB. Следовательно,
NE : EA = PE : EC = KE : EB, откуда KN || AB. Значит, и PM || AB ⊥ BC || KP.
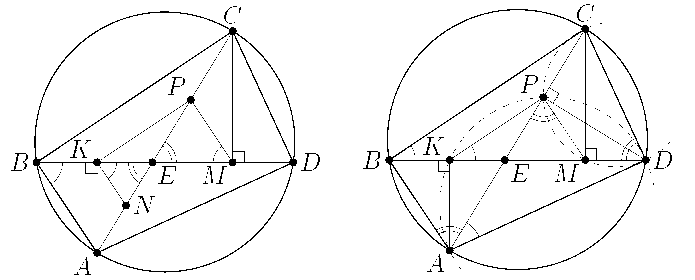
∠AKD = ∠APD = 90°. Из равенства ∠CPD = ∠CMD = 90° следует вписанность четырёхугольника CPMD, откуда
∠EPM = 180° – ∠CPM = ∠EDC = ∠BAC = ∠BAE. Отсюда следует, что PM || AB ⊥ BC || KP. Случай, когда K лежит на отрезке DE, рассматривается аналогично.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь